El álgebra booleana es la
teoría matemática que se aplica en la lógica combinatoria. Las variables
booleanas son símbolos utilizados para representar magnitudes lógicas y pueden
tener sólo dos valores posibles: 1 (valor alto) ó 0 (valor
bajo).
Operaciones Booleanas y
Compuertas Básicas
Las operaciones boolenas son
posibles a través de los operadores binarios negación, suma y multiplicación,
es decir que estos combinan dos o más variables para conformar funciones
lógicas. Una compuerta es un circuito útil para realizar las operaciones
anteriormente mencionadas.
Inversión o negación
(complemento)
El apóstrofe (’) es un
operador algebraico que invierte el valor de una variable, es decir, si X denota
la señal de entrada de un inversor, entonces X’ representa el
complemento de tal señal.
Ecuación
|
Entrada A
|
Salida B
|
B=A’
|
0
|
1
|
1
|
0
|
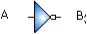
El símbolo lógico de la
negación booleana se representa a continuación
Suma booleana
La suma booleana es 1 si
alguna de las variables lógicas de la suma es 1 y es 0 cuando
todas las variables son 0. Esta operación se asimila a la conexión
paralela de contactos.
Entrada A
|
Entrada B
|
Salida X
|
0
|
0
|
0
|
0
|
1
|
1
|
1
|
0
|
1
|
1
|
1
|
1
|
En circuitos digitales, el
equivalente de la suma booleana es la operación OR y su
símbolo lógico se representa:
Multiplicación booleana
La multiplicación booleana
es 1 si todas las variables lógicas son 1, pero si
alguna es 0, el resultado es 0. La multiplicación
booleana se asimila a la conexión serie de contactos.
La tabla de verdad de la
multiplicación booleana se muestra a continuación:
Entrada A
|
Entrada B
|
Salida X
|
0
|
0
|
0
|
0
|
1
|
0
|
1
|
0
|
0
|
1
|
1
|
1
|
En circuitos digitales, el equivalente de la
multiplicación booleana es la operación AND y su símbolo se
representa:
El inverso de la función AND
es la función NAND. La tabla de verdad se muestra a continuación.
Entrada A
|
Entrada B
|
Salida X
|
0
|
0
|
1
|
0
|
1
|
1
|
1
|
0
|
1
|
1
|
1
|
0
|
El símbolo lógico de la
compuerta NAND se representa a continuación.
FLIP-FLOP
Se trata de un multivibrador capaz de permanecer en
un estado determinado o en el contrario durante un tiempo indefinido. Esta
característica es ampliamente utilizada en electrónica digital para memorizar
información.
Un biestable, también llamado báscula (flip-flop en
inglés), es un multivibrador capaz de permanecer en un estado determinado o en
el contrario durante un tiempo indefinido. Esta característica es ampliamente
utilizada en electronica digital para memorizar información. El paso de un
estado a otro se realiza variando sus entradas. Dependiendo del tipo de dichas
entradas los biestables se dividen en asíncronos y síncronos.
La principal diferencia es que el asíncrono solo
tiene entradas de control, sin embargo el síncrono dispone además de una entrada
para sincronismo o reloj. Si las entradas de control dependen de la de
sincronismo se denominan síncronas y en caso contrario asíncronas. Por lo
general, las entradas de control asíncronas prevalecen sobre las síncronas. La entrada de sincronismo puede ser activada
por nivel (alto o bajo) o por flanco (de subida o de bajada). Dentro de los
biestables síncronos activados por nivel están los tipos RS yD, y dentro de los
activos por flancos los tipos JK,T y D.
FAMILIAS
TTL Y CMOS
La compuerta TTL fue una mejora introducida a la
compuerta DTL. Los parámetros más importantes de las compuertas TTL son el
retardo de propagación (ns), la disipación de potencia (mW), y el producto
velocidad -potencia (pJ). El producto velocidad-potencia indica un retardo en
la propagación con una disipación de potencia determinada.
Familia TTL
(Lógica de Transistor - Transistor)
Esta fue la primera familia de éxito comercial, se
utilizó entre 1965 y 1985. Los circuitos TTL utilizan transistores bipolares y
algunas resistencias de polarización. La tensión nominal de alimentación de los
circuitos TTL son 5 V DC.
Niveles Lógicos
TTL
En el estudio de los circuitos lógicos, existen
cuatro especificaciones lógicos diferentes: VIL, VIH, VOL y VOH.
En los circuitos TTL, VIL es la tensión de entrada
válida para el rango 0 a 0.8 V que representa un nivel lógico 0 (BAJO). El
rango de tensión VIH representa la tensiones válidas de un 1 lógico entre 2 y 5
V. El rango de valores 0.8 a 2 V determina un funcionamiento no predecible, por
lo tanto estos valores no son permitidos. El rango de tensiones de salida VOL,
VOH se muestra a continuación:
Circuitos Lógicos
CMOS (Metal Óxido Semiconductor Complementario)
La tecnología CMOS es la más
utilizada actualmente para la construcción de circuitos integrados digitales,
como las compuertas, hasta los circuitos como las memorias y los
microprocesadores. La tensión nominal de alimentación de los circuitos CMOS son +5
V y +3,3 V.
Niveles Lógicos CMOS
Se muestran las tensiones VIL, VIH,
VOL, VOH válidas para los dispositivos CMOS de
nivel +5 VDC.